Ordering Movie Credits With Graph Theory
How Graphs & Games Untangled "The Golden Hairball"
At Endcrawl we're always thinking about the hard work that goes into making film and TV, and how that work translates to on-screen credits.
A feature film may involve thousands of people, hundreds of distinct job titles or "roles," and dozens of departments. So there's plenty for a producer to worry about, like:
- Did we forget or misspell a name?
- Is this the correct way to credit that role?
- Do all these departments and roles appear in the right order on screen?
Today we'll tackle that last question: how do you order end credits?
This is surprisingly hard to answer. Pick any two films and you'll find conflict in how screen credits are ordered. There are so many minor disagreements, in fact, that a human can't hope to reconcile them. (And there's a terrifying graph farther down to prove it.) You'll need math and computers to make sense of it all.
The other thing you'll need is granular data. Lots of it. And after running over 4,000 films and TV shows through our end credits SaaS, we have that, too. In fact we have higher quality crediting data than anyone on the planet, since Endcrawl's database records are canonical -- the very records used to bake out the final on-screen titles. We also have precise positional and ordering data that no one else has. (Not even that big movie website you're thinking of.)
So we've got a story to tell you about how we used graph theory to untangle the collective wisdom of our filmmaker customers, and to start answering some of the questions they face around properly attributing creative labor.
Before we go on, it's important to note that our Perfect End Credits Template isn't merely the result of an algorithm applied to lots of data. To pull it off, we also had to compile a massive Credits Thesaurus by hand, interview a number of industry experts, and use domain knowledge to shape the final results. But we'll talk about those efforts another day. This post is for anyone who's interested in solutions to hard technical problems -- and especially for those of you who like to stay in the theater until the last credit rolls out. So buckle up.
And let's ease into it with a few examples that are closer to home.
Three Examples from Real End Credits
There are 70 departments and 500+ roles in our Template. That's a lot.
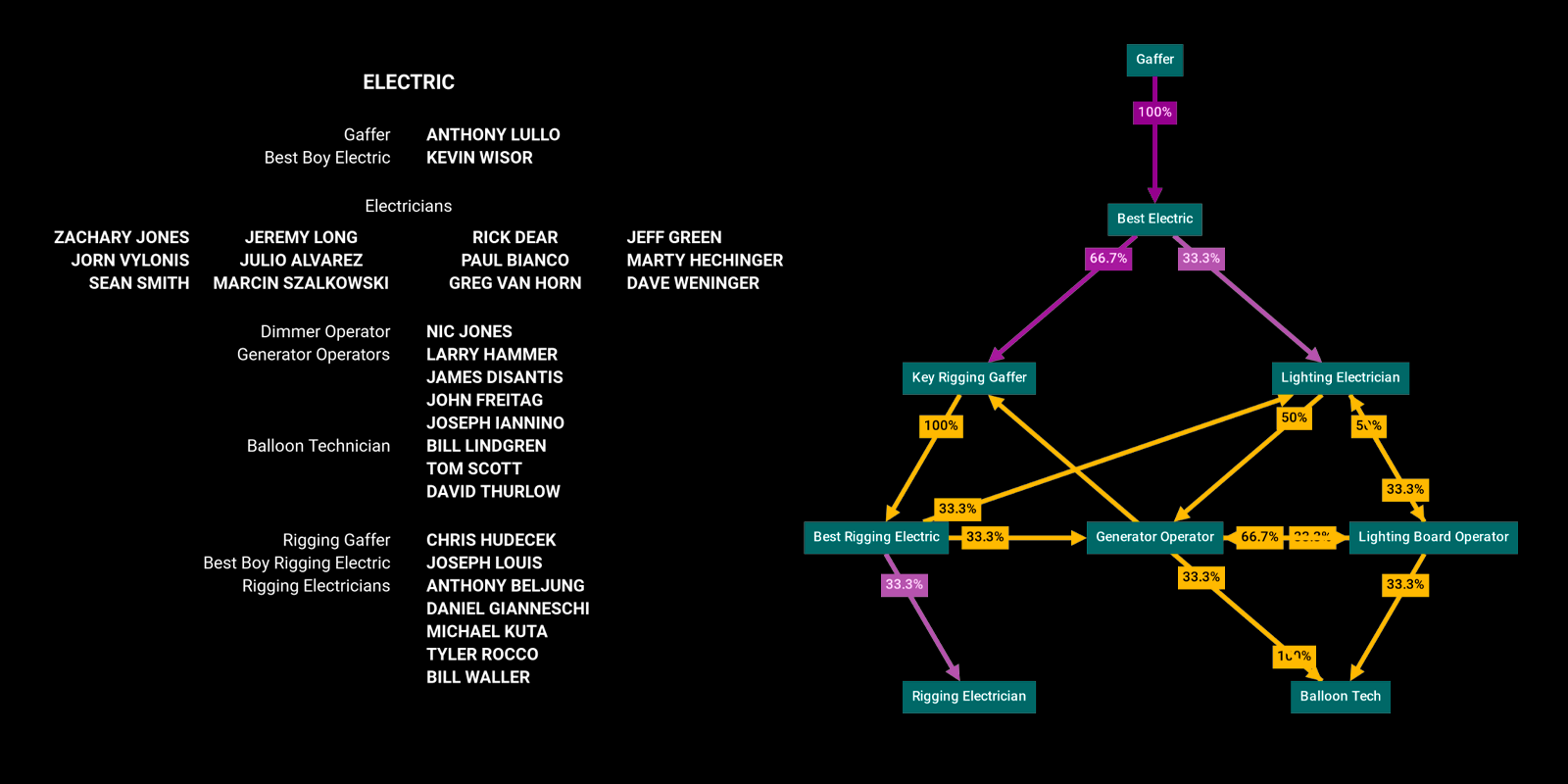
For simplicity, we'll narrow in on one department containing 16 standardized roles: the Electric department. As the name implies, these folks are responsible for all things electricity-related. They generate power, they set up and operate lighting, and they run power to the lights and other things on set.
Example 1: Black Is King
Let's have a look at the Electric department credits for "Black is King", the 2020 visual album from Beyoncé. (All the examples we'll present here used Endcrawl for their end credits.)

In this article we're focusing on roles -- things like Gaffers and Best Boy Electrics. So we'll extract a list of standardized roles in the order they appear on screen, which is what you see in the blue-green boxes.
What are all these roles exactly, and what do they do? A rundown:
- 🕴️ Gaffer -- The Electric department head. They work closely with the Director of Photography to achieve the "look" that the director is after. The word is likely an archaic derivation of godfather meaning "boss" or "chief". (See also: Ted Lasso.) Some think it derives from the "gaff" pole used by Victorian-era lamplighters.
- 🥇 Best Electric -- Reports directly to the Gaffer and is arguably the the second most senior electrician on the crew. They are the on-set electric "foreperson", responsible for executing the gaffer's decisions. Although this job has historically been named Best Boy Electric, we've seen "Best Electric" show up increasingly in credits and in labor union documents. Endcrawl's template defaults to gender-neutral language.
- 🔑 Key Rigging Gaffer -- The "rigging" contingent of the electric crew pre-stages lighting equipment typically days before shooting. The Key Rigging Gaffer is in charge of this group. Arguably, this is the second most senior electrician.
- 🗜 Best Rigging Electric -- Works directly under the Key Rigging Gaffer.
- 💡 Lighting Electrician -- Sometimes just called Electrician, Electric, Lighting Technician, or Spark. This is the core contingent of the lighting department. They are responsible for running power to everything on set: not just lights, but also monitors, trailers, and coffee makers.
- 🔋 Generator Operator -- Sometimes Genny Operator or just Genny Op, this person provides power when regular "house power" is either unavailable or not up to the task.
- 🕹️ Lighting Board Operator -- This role goes by a variety of names like Dimmer Board Operator, Console Operator, or Console Programmer. They're in charge of a control console with lots of buttons. Buttons that make the lights do cool things.
- 🎈 Balloon Tech -- When you need large amounts of diffuse light, especially on a huge set with tall ceilings, simple China Balls won't cut it. Enter the balloon tech, who operates large helium lighting balloons.
Is this the standard ordering for the Electric department? To find out, let's look at another example.
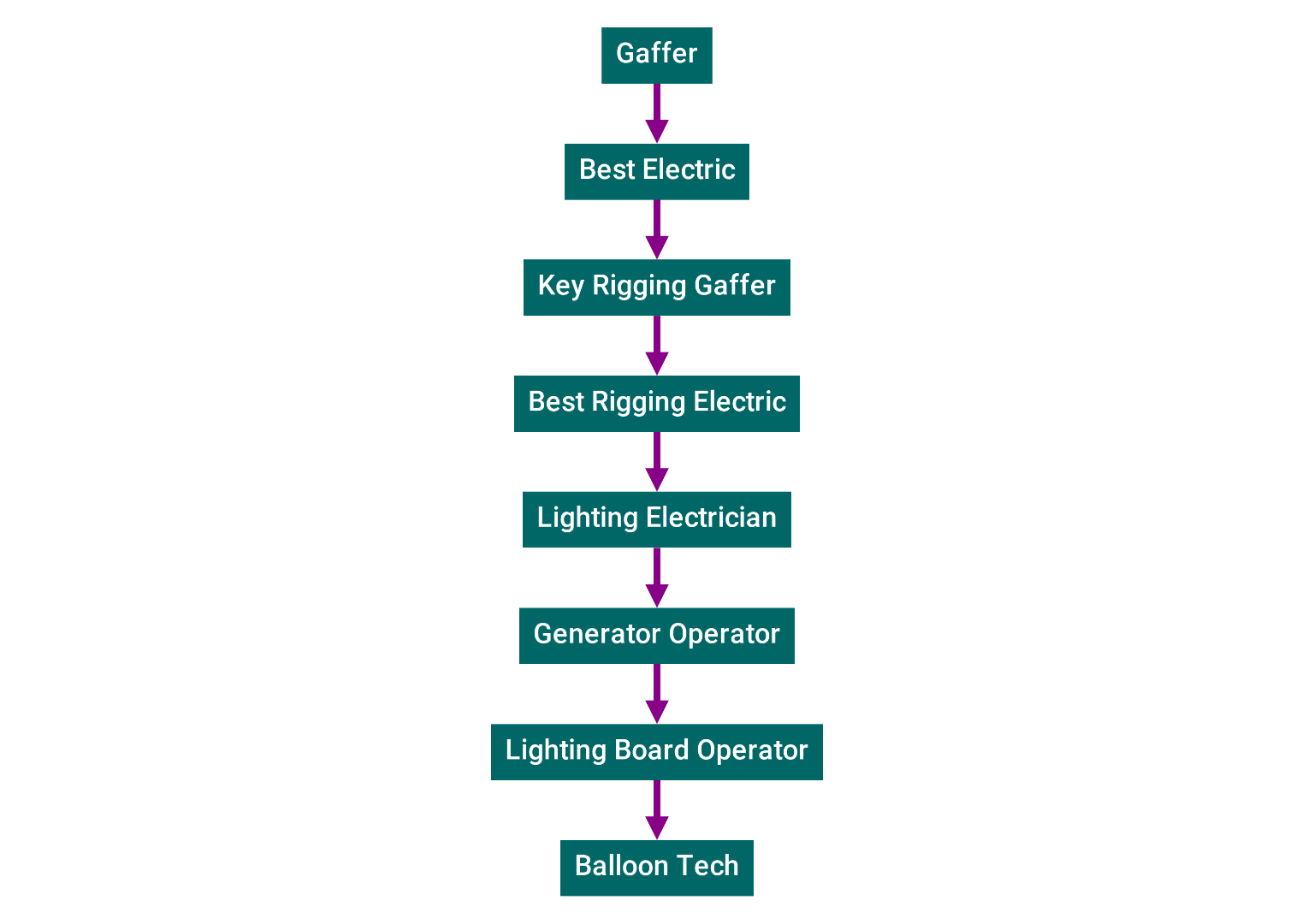
Example 2: Love Hard
Here's the Electric department from "Love Hard", a Christmas romcom that spent 5 weeks in the Netflix top 10 films list.


At first glance, the list of standardized roles looks the same. But look closer...
There's a small disagreement: this time, Lighting Electrician appears last. In the previous example it preceded Generator Operator. Which one is right?
Examples 1 + 2: Things Start to Get Interesting
Let's see what happens when we combine the orderings from the previous two examples:
You'll notice the magenta lines with arrows -- called edges -- now have labels with numbers telling us how likely a role is to follow another one.
The golden edges are part of a cycle. If you're following the edge arrows from role to role, you can end up traveling in a loop:
- 💡 Lighting Electrician ➡️
- 🔋 Generator Operator ➡️
- 🕹️ Lighting Board Operator ➡️
- 💡 Lighting Electrician -- and we're back to where we started 🔁.
This cycle is a problem for us because a loop has no clear ordering. Every role comes before every other role. But it also comes after every role, if you keep going around. And around we go.
Would a third example help clear things up?
Example 3: Chi-Raq
Here's the Electric Department from Spike Lee's 2015 film "Chi-Raq".

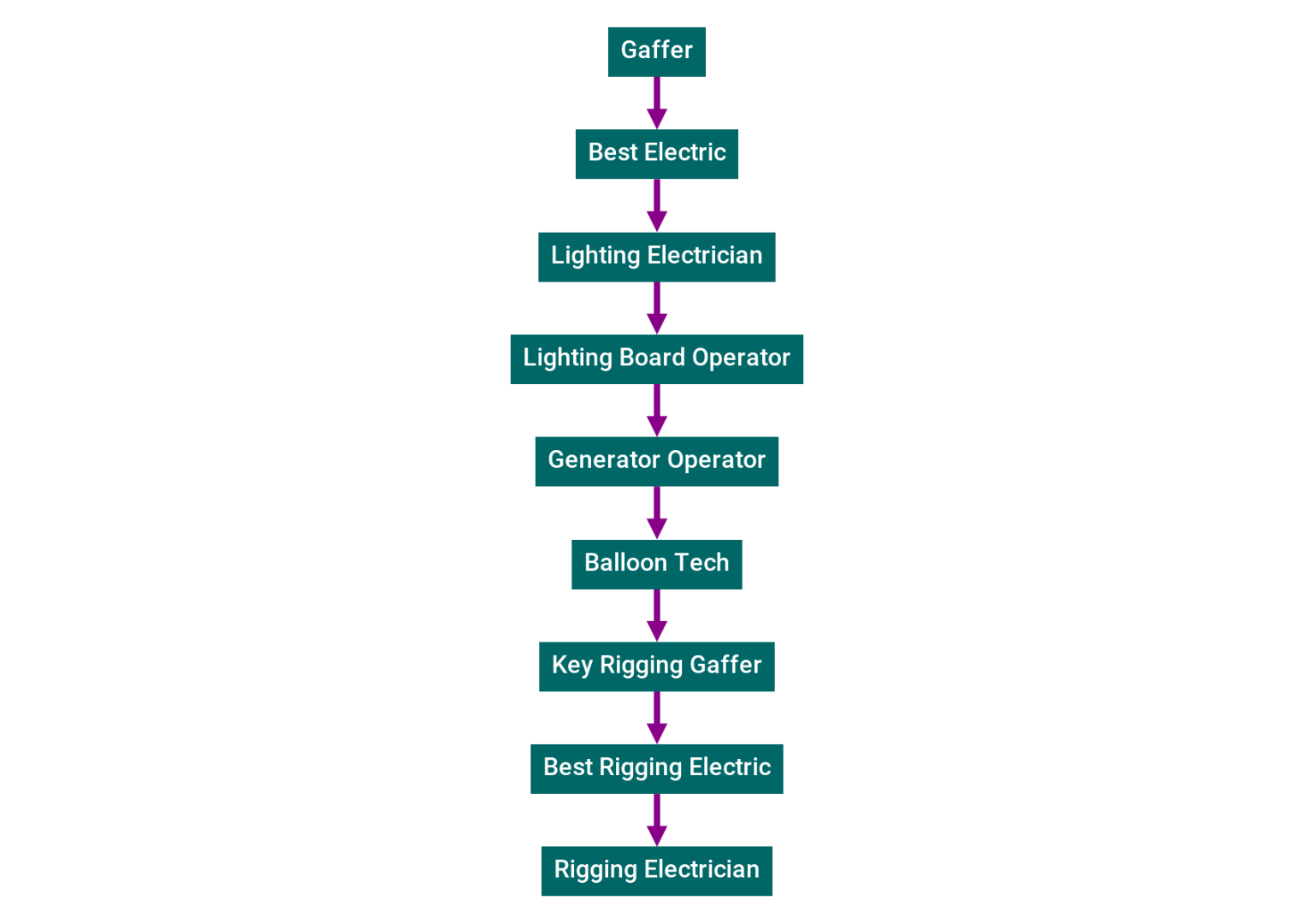
This time, the Balloon Tech role appears midway through instead of at the very end, so you can probably already sense trouble. Let's combine all three example orderings and see.
Examples 1 + 2 + 3: The Plot Thickens
The golden cycle mess got bigger! There's even more uncertainty in the ordering than before.
Full disclosure: what we're showing you here is known as a graph, a mathematical structure that consists of nodes and the edges that connect them. In fact, even the role ordering from Black is King above -- where the nodes form a sort of vertical congo line -- was a basic graph. 1
We may have started out with nice vertical lines, but the graphs are getting fatter as we combine more examples. As they lose their sense of clear ordering, they also lose their top-to-bottom-ness. When this happens we'll start using a circular graph layout. Click the interactive graph above see it animate between layouts.
All Examples Combined: The Golden Hairball
Thousands of film & TV productions have used Endcrawl. Combining the Electric department orderings for all of them gets us this...
Yikes. The mess is now a veritable snake pit. As you can see, we've had to switch to a circular graph layout, since most of the edges are now part of golden cycles, and there's no real "top" or "bottom" anymore. Our clear Electric department ordering has gone from obvious to seemingly nonexistent.
How do we get out of this mess? Is a clear ordering even possible?
It turns out it is. But getting there involved many dead-ends, a graph theory deep dive, a recent research paper, and -- unexpectedly -- the XBox player rating system. Read on.
The Problem
A good problem definition is worth a thousand solutions.
-- Me
Now we can state the problem.
Given thousands of example orderings for roles in credits, many of which have disagreements, how can we find the "best" ordering?
The same thing, said in math: given a directed graph with cycles, find an ordering of the nodes which minimizes a cost function.
Chasing a Solution
We need something that takes a messy set of example orderings as input, then outputs each role exactly once in some order. In other words, we're looking for an algorithm.
What Even is a "Best" Ordering?
Before we start experimenting with algorithms, how do we define this "best" ordering? Without that, we don't know if we're headed in the right direction, much less whether we've arrived. We need a compass. To fashion one, suppose there were only 3 roles in the Electric department, and this was their correct order:
- 🕴️ Gaffer
- 🥇 Best Electric
- 💡 Lighting Electrician
If the algorithm outputs...
- 🥇 Best Electric
- 🕴️ Gaffer
- 💡 Lighting Electrician
...then the algorithm is wrong and should be punished. Best Electric and Gaffer are swapped. But hang on, it's also kinda right, too: it correctly put Lighting Electrician in the 3rd slot. Can we quantify how wrong the algorithm is?
We can, and one way to measure that is the permutation distance 2 between the algorithm's output and the correct ordering. There are lots of ways to do this; we'll pick one called Squared Deviation Distance (SDD).
In the above example, SDD tells us we're (-1)*(-1) + 1*1 + 0*0 = 2 away from the correct ordering. If the algorithm nailed it, the distance would be 0*0 + 0*0 + 0*0 = 0. Lower is better, and a measure of zero is best.
Each of the following experiments will yield a candidate for "best" ordering. Since we don't know the correct ordering yet, we'll grade the experiment by reporting its average permutation distance to the example orderings. 3 Alas, since the example orderings don't fully agree, an overall SDD grade of 0 is out of reach. How low can we go? We don't know, and we may hit a limit. To distinguish similar SDDs that may be near the limit, we'll also report a subjective human grade.
Experiment 1: Brute Force Search
When in doubt, use brute force.
-- Ken Thompson
Speaking of permutation distance, what if the algorithm simply searched for the ordering that yielded the smallest total distance against all the ordering examples? By definition this ordering is "best."
Unfortunately, permutation search space is big. Really big, like O(N!) big.
To make this concrete, we've identified 16 standardized roles in the Electric department, so we'd need to check 16! = 20,922,789,888,000 different orderings. That's 21 trillion permutations to check. We'd be here all day. 4
It gets worse for large departments. Sound Post-Production, with its 93 standardized roles, would involve checking 1 x 10 ^ 144 possible orderings. That's far more than the estimated number of atoms in the universe. We'd be here until the lights went out.
Sorry Ken, this one's a no-go.
Grade (SDD): does not compute
Grade (Human): Incomplete
Experiment 2: Average Position
What if we averaged the position of each role across all the ordering examples, then sorted the roles by average position?
For instance, if Gaffer appears 1st, 2nd, 1st, and 1st in your 4 examples, it would have an average position of (1 + 2 + 1 + 1) / 4 = 1.25. That would guarantee it the first place spot in the final algorithmic ordering.
This does seem to work okay for the first few roles in the department. Things start to fall apart in the middle, a failure mode we called the "muddy middle". Here's the ordering, together with each role's average position:
- 🥇 Best Electric (
0.2696) - 🕴️ Additional Gaffer (
0.2821) - 💡 Lighting Electrician (
0.3106) - 🕴️ Gaffer (
0.3401) - 🔋 Generator Operator (
0.3668) - 🛋️ Lamp Operator (
0.3739) - 🪚 Shop Electric (
0.3744) - 🪢 Rigging Electrician (
0.3765) - 🎓 Electric Intern (
0.3798) - ⚡ Additional Electric (
0.3881) - 🕹️ Lighting Board Operator (
0.3911) - 🔑 Key Rigging Gaffer (
0.4190) - 🏕️ Basecamp Electrician (
0.4229) - 🎈 Balloon Tech (
0.4382) - 🔋 Basecamp Generator Operator (
0.4537) - 🗜 Best Rigging Electric (
0.4836)
Squinting at the average positions for these middle roles, we see plenty of near-ties that only differ in the 3rd decimal place (0.3739, 0.3744, 0.3765, 0.3798). There isn't much useful positional information in these tiny fluctuations -- we realized we were squinting at noise.
Placing Best Rigging Electric last is also utter nonsense.
Grade (SDD): 0.49
Grade (Human): F
Experiment 3: PageRank
The next thing we reached for was PageRank, the famous algorithm at the heart of Google.
To apply PageRank to credits, imagine each role is a page. If Best Electric comes immediately after Gaffer, we'll pretend a page Best Electric links to a page Gaffer.
PageRank tells you what pages you're likely to land on if you click links at random. We thought applying PageRank to credits might tell you what roles you're most likely to land on, and that would give you an ordering. And we know PageRank is fine with cycles (webrings, anyone?).
So we tried it with all Electric department roles, and it was our first real breakthrough. Here's the ordering, together with the PageRank score for each role:
- 🕴️ Gaffer (
0.2607) - 🥇 Best Electric (
0.2177) - 💡 Lighting Electrician (
0.1526) - 🔑 Key Rigging Gaffer (
0.0985) - 🔋 Generator Operator (
0.0652) - 🕹️ Lighting Board Operator (
0.0454) - 🗜 Best Rigging Electric (
0.0442) - 🪢 Rigging Electrician (
0.0374) - 🛋️ Lamp Operator (
0.0259) - 🪚 Shop Electric (
0.0155) - 🏕️ Basecamp Electrician (
0.0096) - 🕴️ Additional Gaffer (
0.0083) - 🔋 Basecamp Generator Operator (
0.0064) - 🎈 Balloon Tech (
0.0063) - 🎓 Electric Intern (
0.0046) - ⚡ Additional Electric (
0.0016)
Alas, although it starts and ends well, on closer inspection we saw a similar "muddy middle" problem. Does it make sense that Key Rigging Gaffer is separated from Best Rigging Electric by several unrelated roles? That the generalist Lighting Electrician role landed in the third slot? Or that Shop Electric is thrown randomly into the middle of things?
Grade (SDD): 0.10
Grade (Human): B-
Experiment 4: Breaking Cycles Naïvely
The last two experiments suffered from the muddy middle problem. We theorized that they threw away too much graph structure, and that "fine" graph structure was somehow essential to ordering.
Specifically, we wondered if we could remove the "worst" edges of a graph, returning it to a directed acyclic graph (DAG)? In theory we'd only need to concentrate on removing golden edges, since the magenta edges never participate in a cycle. Here's that graph from examples 1 + 2 + 3 again:
To see why a DAG helps, let's touch on topological sorting. This takes a graph -- and not just any graph, it must be a DAG -- and orders the nodes so that the edges always point forward. For instance, here's a DAG together with a topological sorting of its nodes:
And here's the same DAG with a different, but equally valid, topological sorting:
Since there are many ways to topologically sort a DAG, it can't take us all the way to a solution. But it does get us closer. And from there, a clear ordering might be within reach.
How do we decide which golden edges to remove on the way to a DAG? Since we're trying to preserve graph structure, ideally we'd remove as few edges as possible. This idea sounds great in theory! Unfortunately, the theory has decided our idea is awful: this is known as the minimum feedback arc set problem, and it's NP-hard. We'd be waiting days (or decades).
So that's out. We considered various naïve strategies for edge removal. One of these strategies was "take from those who have the most": nodes with lots of edges could afford to have some of their edges removed. This eventually got us to a DAG, but not before removing 188 of the 198 total edges! There was very little graph left.
Despite that, the ordering looks okay:
- 🪚 Shop Electric
- 🕴️ Gaffer
- 🕴️ Additional Gaffer
- 🥇 Best Electric
- 🔋 Generator Operator
- 💡 Lighting Electrician
- 🏕️ Basecamp Electrician
- 🎈 Balloon Tech
- 🎓 Electric Intern
- ⚡ Additional Electric
- 🔑 Key Rigging Gaffer
- 🗜 Best Rigging Electric
- 🪢 Rigging Electrician
- 🛋️ Lamp Operator
- 🕹️ Lighting Board Operator
- 🔋 Basecamp Generator Operator
But there are some questionable choices here. Why on earth is Shop Electric first? Does Basecamp Generator Operator deserve to be last, or might it be better grouped with Basecamp Electrician or Generator Operator? Should Balloon Tech and Electric Intern appear midway through, ahead of the rigging roles? Something still wasn't right.
Grade (SDD): 0.11
Grade (Human): B+
Experiment 5: Breaking Cycles in Noisy Hierarchies
We cast about for other ways to turn cyclic graphs into acyclic ones. The search turned up a research paper from 2017 titled "Breaking Cycles in Noisy Hierarchies". The paper's code is opensource, and it uses the excellent python graph analysis library networkx we'd used in the previous two experiments.
It wasn't clear at first whether this paper applied to the problem of ordering credits. It opens by discussing taxonomy graphs and ontology. But farther in, there are experimental results on a variety of datasets: the Google web graph, messaging graphs, even the expertise graph of Q&A sites like StackOverflow. Might end credits involve the same kind of noisy but hierarchical structure? It seemed plausible.
First we adapted the paper's code into a simple python program. Like the solution we're after, this program takes a stream of example orderings, combines them into a single directed graph, and then starts removing edges to break cycles. Once all the cycles are broken and we have a DAG, it uses topological sorting plus tiebreaking to find an ordering. Here's the program in its entirety:
import networkx as nx
import sys
def main():
graph = build_graph(sys.stdin)
for v in inferred_ordering(graph):
print(v)
def inferred_ordering(graph):
ranks = rank_nodes(graph)
removals = remove_edges_greedily(graph, ranks)
graph.remove_edges_from(list(graph.selfloop_edges()) + removals)
tiebreaker = lambda v: -ranks[v]
ordering = nx.lexicographical_topological_sort(graph, key=tiebreaker)
return reversed(list(ordering))
def rank_nodes(graph):
return dict(graph.degree())
def remove_edges_greedily(graph, ranks):
removals, sccs = [], nontrivial_sccs(graph)
costs = dict([ ((u,v), ranks[u]-ranks[v]) for u,v in graph.edges() ])
while sccs:
subgraph = sccs.pop(0)
max_cost_edge = max(subgraph.edges, key=lambda edge: max(costs[edge],0))
removals.append(max_cost_edge)
subgraph.remove_edge(*max_cost_edge)
sccs += nontrivial_sccs(subgraph)
return removals
def nontrivial_sccs(graph):
return [ scc for scc in scc_subgraphs(graph) if len(scc.nodes) >= 2 ]
def scc_subgraphs(graph):
return [ graph.subgraph(scc).copy() for scc in nx.strongly_connected_components(graph) ]
def build_graph(stream):
graph, last_example, last_item = nx.DiGraph(), None, None
for line in stream:
example, item = line.rstrip('\n').split('\t')
if example != last_example:
last_item = None
if last_item:
graph.add_edge(item, last_item)
last_example = example
last_item = item
return graph
if __name__ == '__main__':
main()
Considering all the work it's doing, this code is short and sweet. (Thanks again networkx!)
However: the function rank_nodes is an impostor. Right now it says nodes with more total edges -- both incoming and outgoing -- rank higher. In reality this is a poor measure of hierarchical rank. For a better ranking algorithm, we'll turn to the paper, which considers two different possibilities.
1. Ranking by Social Agony
One ranking algorithm discussed in the paper is called Social Agony: "It's assumed that in social networks such as Twitter, agony can be caused when people follow other people who are lower in the hierarchy." While agony may have other causes on Twitter -- such as opening the app, or reading a tweet -- the authors of the original Social Agony paper had a precise mathematical definition in mind. Here it is for fun:

Social Agony finds a ranking that minimizes the number of "backwards" edges. The Social Agony paper was written in the heyday of social networks nearly a decade ago, and unfortunately the code was both a little hard to find, and a little hard to compile. Instead we skipped ahead to...
2. Ranking by TrueSkill
The other ranking algorithm used in the paper is called TrueSkill, and it comes to us by way of checks notes ... gaming? It says here it comes from gaming.

TrueSkill was developed by Microsoft Research to rank XBox Live players. To get an intuition for how it works, consider two players in head-to-head matches.
| Match | Outcome | TrueSkill Odds | |
|---|---|---|---|
| 50% - 50% | |||
| 1 | win: player 1 | → | 77% - 23% |
| 2 | win: player 1 | → | 87% - 13% |
| 3 | win: player 2 (!) | → | 53% - 47% |
| 4 | win: player 1 | → | 73% - 27% |
Before they've faced each other, the players are 50-50; TrueSkill knows nothing. After 2 straight wins, TrueSkill thinks player 1 is likely to win the 3rd match. But there's an upset, and TrueSkill revises the odds almost back to even. Even though player 1 wins the final match, their odds don't quite bounce back to those early, undefeated heights.
You can think of TrueSkill as a way to measure "surprise" in iterated games. If a loss would be surprising, you rank higher. If a loss would be unsurprising, you rank lower. Initially TrueSkill isn't very sure of the rankings, but as it sees more and more matches between the same players, the rankings become more certain -- and upsets become more surprising.
This intuition may translate over to end credits. If, after looking at the credits for thousands of productions, it's surprising for role A to appear immediately after role B, we could say role A ranks higher. It's also a good omen that we've been constructing graphs throughout this analysis in a similar way -- adding edges whenever role A immediately precedes role B.
To top it off, TrueSkill has a nice opensource python implementation. All this to say: we decided to use TrueSkill to break cycles.
Breaking Cycles with TrueSkill
TrueSkill, it turns out, is a good cycle breaker. It was much better at preserving graph structure than the naïve strategies. Instead of removing 95% of edges, TrueSkill removed half of all edges before arriving at a DAG. Maybe this still sounds like a lot, but think back to the Golden Hairball. Half of all edges is a small price to pay.
The resulting graph is acyclic as promised, but has lots of superfluous magenta edges. These make it difficult for a human to see the graph's backbone. Or anything, really:
What do we really mean by "superfluous" edges? Well, if there's a well-worn path directly from node A to node D, then we probably don't need the more roundabount path A -> B -> C -> D. A formal version of this idea is the minimum spanning tree (MST) -- or in our case, a slight variation called the maximum spanning tree.
After applying MST to the graph above, the following leaps off the page:
This was astonishing to see! 5 Some immediate observations:
- 🌲 Thanks to MST, it's no longer a graph, but more specifically a tree.
- 🕴️ Gaffer is the star on this christmas tree, as it should be. It almost always comes first.
- 🕴️ Additional Gaffer is a solitary offshoot that appears directly under Gaffer, which makes sense.
- 🥇 Best Electric immediately follows Gaffer, and is the main conduit to the rest of the tree.
- 🔑 Key Rigging Gaffer has two other Rigging roles that commonly appear after it.
- 🔋 Generator Operator is grouped with Basecamp Generator Operator, which makes semantic sense.
- 💡 Lighting Electrician is the gateway to other Electrical roles, and to the rarer Balloon Tech.
As alluded to in topological sorting, there are still many possible orderings of this tree. We'll need to choose from among them. The observations above, however, have already given us some clues.
Gaffer is unambiguously first. The next question is whether to go left or right.
If we go right and pick Best Electric, then we'll have to return to Additional Gaffer at some later point, probably after exploring everything under Best Electric. It doesn't make sense to separate Gaffer and Additional Gaffer -- if the latter appears, it's best to list it immediately, then continue with the weightier subtree starting with Best Electric.
This can be extrapolated into a general rule: when faced with a branching choice, prefer "lighter" subtrees to "heavier" ones. Subtree weight could simply be node count -- or, it could be something more nuanced like the total TrueSkill rating of its nodes.
We tried both, and total TrueSkill rating got us slightly better results. Here's the ordering:
- 🕴️ Gaffer
- 🕴️ Additional Gaffer
- 🥇 Best Electric
- 🛋️ Lamp Operator
- 🏕️ Basecamp Electrician
- 🕹️ Lighting Board Operator
- 🔋 Generator Operator
- 🔋 Basecamp Generator Operator
- 🔑 Key Rigging Gaffer
- 🗜 Best Rigging Electric
- 🪢 Rigging Electrician
- 💡 Lighting Electrician
- ⚡ Additional Electric
- 🎈 Balloon Tech
- 🎓 Electric Intern
- 🪚 Shop Electric
This ties our best score, and the ordering makes intuitive sense too.
Grade (SDD): 0.10
Grade (Human): A-
Results and Future Directions
We set out to order end credits from real examples -- thousands of films & TV shows, with lots of minor ordering disagreements -- and fared well, all things considered. There are more sources of noise we could eliminate, and more algorithmic improvements we could make. In the end we think a "correct" ordering for the 16 standardized Electric department roles looks something like this:
- 🕴️ Gaffer
- 🕴️ Additional Gaffer
- 🥇 Best Electric
- 🛋️ Lamp Operator
- 🔋 Generator Operator
- 🔋 Basecamp Generator Operator
- 🕹️ Lighting Board Operator
- 💡 Lighting Electrician
- 🏕️ Basecamp Electrician
- ⚡ Additional Electric
- 🎓 Electric Intern
- 🔑 Key Rigging Gaffer
- 🗜 Best Rigging Electric
- 🪢 Rigging Electrician
- 🎈 Balloon Tech
- 🪚 Shop Electric
If we measure distance to this "correct" ordering instead of measuring against the noisy example orderings, these are the final grades:
- Experiment 1 Grade (SDD):
does not compute - Experiment 2 Grade (SDD):
0.22 - Experiment 3 Grade (SDD):
0.31 - Experiment 4 Grade (SDD):
0.41 - Experiment 5 Grade (SDD):
0.12
The Perfect End Credits Template
The obvious next step is to apply this to the other 70 departments! And that's exactly what we've done with The Perfect End Credits Template.
How this will evolve
This is a work in progress, and we'll continue to revise it as we learn more.
We're also looking at automatically structuring and ordering raw job data for our customers. Today the typical Endcrawl customer turns over an ordered list of credits to us. In the future, customers can hand off a flat list of jobs, and Endcrawl will be able to standardize, structure, and order it for them -- another small step towards democratized filmmaking.
With our data together with this algorithm, we can quickly react to the changing times. Crediting conventions evolve, new roles appear, and Endcrawl can help its customers stay on top of it all. Although Gaffer dates back to the Victorian era, we frequently see new roles appearing in credits. Consider that COVID Compliance Officer didn't appear a single time in credits 18 months ago. Now it's credited in hundreds of Endcrawl productions -- and we know exactly where it goes.
Thanks for sticking it out. We hope you enjoyed this little break from your work day. May you always receive proper credit for your labor.
Until next time,
Credits & Acknowledgments
Special thanks to the authors of "Breaking Cycles in Noisy Hierarchies": Sun, Ajwani, Nicholson, Sala, and Parthasarathy. Bet you didn't see this one coming!
Thanks to The Endcrawl Team for feedback and support. Thanks to Rod Bogart, Eric Switzer, Paul Shapiro, Ethel, Jacob, Alex, Julianne, and the others who read drafts.
All the interactive graphs were made with cytoscape.js. Graph analysis was done with networkx. Kudos to Microsoft Research and the TrueSkill project.
Footnotes
-
And we're certainly not the first ones to apply graph theory to movie credits! Six Degrees of Kevin Bacon, anyone? ↩
-
There are many possible metrics for permutation distance. Here's a paper analyzing a boatload of them. Levenshtein Distance is one, although it's
O(N^2). We chose Squared Deviation Distance (SDD) because it'sO(N)and simple to implement. ↩ -
The Grade (SDD) reported for each experiment is a weighted average of the normalized permutation distance between the candidate ordering and each example ordering. The candidate ordering is always 16 elements long, but example orderings are often just 2 or 3 elements long. So we compute an SDD on the intersection of the two, dividing by the maximum possible SDD between two permutations of that length to normalize into
[0,1]. We then use a weight equal to the length. That way, longer ordering agreements are rewarded more than shorter ones. ↩ -
Are there ways to speed up permutation space search? It sounds like gradient descent on permutation spaces is a thing. I don't know whether these techniques apply to our case. Please reach out if you know! ↩
-
A word of caution: the final Electric department tree isn't necessarily an org chart. It's a map of how Electric department credits occur on screen together. Any similarity to actual organizations, living or dead, is purely coincidental. ↩